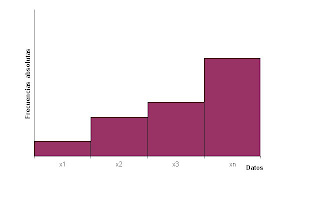
MEDIDAS DE ASIMETRIA SESGO: es el grado de asimetría o falta de asimetría, de una distribución. Si el polígono de frecuencias suavizado de una distribución tiene una cola mas larga a la derecha del máximo central que a la izquierda, se dice que la distribución esta sesgada a la derecha o que tiene sesgo positivo (asimetría positiva) y si es al contrario se dice que tiene sesgo negativo (asimetría negativa)COMENTARIO: El sesgo representa a que lado de la curva están concentrados los datos más representativos. Los sesgos de definición son los que se cometen en el momento de planificar y preparar laencuesta o estudio. Básicamente podemos cometer errores sistemáticos debidos a la fuentede financiación, a la información previa disponible y a la planificación del trabajo:a) Sesgos presupuestarios: son debidos a la influencia de la financiación sobre el proyecto.Parte de la investigación epidemiológica está financiada por empresas u organismos cuyoobjetivo puede ser demostrar o validad alguna decisión que se ha tomado o se desea tomar.Ello supone que en algún caso puede concederse excesiva importancia a ciertos aspectos y

CUTOSIS Y ASIMETRIA

CURTOSIS: la curtosis es la agudeza de la curva normal, esta agudeza puede ser alta, baja o intermedia dando lugar a diferentes tipos de curvas: leptoculticas, platicurticas y mesocurticas.Para calcular la curtosis se utiliza el parámetro B2 si el valor de dicho parámetro es 3, se considera que la curva es mesocurtica, Si es mayor que 3 la curva es Leptocurtica y si es menor que 3 la curva es Platicurtica.Otra medida de curtosis que se puede emplear, esta basada en los cuartiles y percentiles y esta dada por la formula: la base que utilizaremos acá será 0.263 La curtosis es la medida de asimetria la cual esta representando que tan alta son los datos que representa, mostrando el rango de cada uno.

CURTOSIS

Definición de curtosisEl cuarto momento estándar se define como , donde μ4 es el 4º momento centrado sobre la media y σ es la desviación estándar. Esta es la definición de curtosis que se suele emplear en libros antiguos, pero no es la que se expondrá aquí.Comúnmente se define la curtosis comotambién conocida como exceso de Andre. La sustracción del 3 al final de la fórmula se explica generalmente como una corrección que se hace a la curtosis de una distribución normal igual a cero. Otra razón se obtiene examinando la fórmula de la curtosis de la suma de variables aleatorias. Si Y es la suma de n variables aleatorias estadísticamente independientes, todas con igual distribución X, entonces , complicándose la fórmula si la curtosis se hubiese definido como .
El coeficiente de curtosis mide cuan 'puntiaguda' es una distribución respecto de un estándar. Este estándar es una forma acampanada denominada 'normal', y corresponde a una curva de gran importancia en estadística.

DIAGRAMA DE DESPERCION

ESTE DIAGRAMA NOS MUETRA UNA LINEA PUNTO PENDIENTE

REGRECION LOS CLACOS FINANCIEROS

SI NOSOTROS TENMOS ALGUNOS PUNTUS COMO ONANUBE DE PUNTOS ES NECESARIO HACER UNA LINEA CURVA. Y VA SER UNA LINEA EXPUNENCIAL

EXPONENCIAL
CRECIENTE
CUADRATICA

DECRECIENTE

ES MUY IMPORTANTE GRAFICAR LA LINEA DE DISERCION XQ EN ELLA SE DETERMINA LA LINE EXPONENCIAL

REGRECION

X Y

3 5

4 10

5 15

7 18

8 25

9 31

10 40

FORMULA PUNTO PENDIENTE

Y2-Y1=M(X2-X1) PENDIENTE -------M=AY/AX

P(X,Y)

COLUMNAS MARGINALES

ESTA PASO FUE EL SIGUIENTE Q SE HISO DESPUES DE LA TABLA DE DOS ENTRADAS

TABLA DE DOBLE ENTRADA

curtosis

la curtosis la vamos a utilizar si la ditribucion es normal. mide cuantifica la agudeza de la distribucion o fenomenoEl cuarto momento estándar se define como , donde μ4 es el 4º momento centrado sobre la media y σ es la desviación estándar. Esta es la definición de curtosis que se suele emplear en libros antiguos, pero no es la que se expondrá aquí.
Comúnmente se define la curtosis como

tipos de segos

Sesgo de selección: Grupos no comparables debido a cómo se eligieron los pacientes o sujetos.
Sesgo de Información: Grupos no comparables debido a cómo se obtuvieron los datos.
Sesgo de confusión: Existe una mezcla de efectos debido a una tercera variable (variable de
Sesgo retrospectivo o sesgo de a posteriori: es la inclinación a ver los eventos pretéritos como predecibles.
Sesgo de correspondencia, denominado también error de atribución: es la tendencia de hacer excesivo énfasis las explicaciones fundamentadas, comportamientos o experiencias personales de otras personas.
Sesgo de confirmación: es la tendencia a investigar o interpretar información que confirma preconcepciones.
Sesgo de autoservicio: es la tendencia a reclamar más responsabilidad para los éxitos que por los fallos. Se muestra también cuando la gente tiende a interpretar como beneficiosa para sus propósitos información ambigua.(Roy=Cere

sesgo

mide la desviacion que se va dando en la distribucion de tendencia central

HISTOGRAMA PARA DATOS AGRUPADOS

HISTOGRAMA

ESTE HISTOGRAMA SOLO SE HACE CON DATOS AGRUPADOS

El área de cada rectángulo nos da la frecuencia del intervalo, por tanto la base es la amplitud y la altura la densidad de frecuencia de dada uno di

DIAGRAMA DE BARRAS ACUMULADO PARA DATOS AGRUPADOS

DIAGRAMA PARA DATOS AGRUPADOS

DIAGRAMA EN ESCALERA PARA DATOS NO AGRUPADOS

DIAGRAMA DE RECTANGULOS

DIAGRAMA DE RECTANGULOS

DIAGRAMA DE BARRAS

Diagrama de barras Datos sin agrupar y las barras proporcionales a las frecuencias.

TIPIFICACION

Tipificar una variable es cambiarla por otra que tenga de media cero y desviación típica 1. Se utiliza para comparar distribuciones .

Cada valor se tipifica restando la media y dividiendo por la desviación típica, la nueva variable z, tiene de media cero y desviación típica 1.

DESVIACION TIPICA

Es la raíz cuadrada positiva de la varianza y es la medida de dispersión más utilizada.


Clases de medidas de dispersión relativas
Se caracterizan por ser adimensionales, las más importante es el coeficiente de variación de Pearson, nos indica la mayor o menor homogeneidad de los datos respecto de la media y por lo tanto nos da la representatividad de la media en la distribución

VARIANZA

La varianza siempre es mayor o igual que cero. Tan solo hay un caso en que es cero y es cuando todos los valores de la variable son iguales.

Si a los valores de la variable le sumo una constante, la varianza de la nueva variable es la misma que la que tenía antes.
Siempre es positiva (por estar al cuadrado). Como la varianza es siempre positiva, a mayor varianza mayor será la dispersión.

MEDIDAS DE DESVIACION

DESVIACIÓN MEDIA

Es la suma de los valores en valor absoluto de la diferencia entre cada valor de la variable y la media aritmética por su frecuencia y dividido por el número de datos.

CUARTILES

CUANTILES

Son medidas de posición que no tiene porqué ser central. Hay varios tipos de cuantiles:

1.- Cuartiles Son valores de la variable que dividen a la distribución en cuatro partes iguales, por lo tanto los cuartiles son tres C1 que deja por detrás de él al 25% de la población, C2 que divide a la población en dos partes iguales y C3 que deja dtrás de él al 75% de la población.

2.- Deciles Son valores e la variable que dividen a la distribución en diez partes iguales, por lo tanto los deciles son nueve, D1 deja al 10% antes, D2 al 20% y así sucesivamente hasta D9 que deja al 90% antes y al 10% después de él.


3.- Percentiles.- Son valores de la variable que dividen a la distribución en cien partes iguales, por lo tanto los percentiles son 99.
En realidad tanto cuartiles como deciles se calculan con el correspondiente percentil

MODA

MODA

Es el valor de la variable que más veces se repite. En algunos casos existen varias modas, pero normalmente es una, si son dos se llama bimodal.

Para datos no agrupados

La moda es el valor de la variable correspondiente a la mayor frecuencia absoluta.

Para datos agrupados en intervalos

Se halla la densidad de frecuencia de cada uno de los intervalos (di) y el de mayor densidad de frecuencia se selecciona como intervalo modal, para determinar el valor de la Moda, se aplica la siguiente fórmula, basada en la proporcionalidad:

2.- MEDIANA

Es el valor de la variable que ocupa el lugar central de la distribución, es decir el valor de la variable que deja el 50% de observaciones hacia la izquierda y el 50% a la derecha.

Para poder hallar la mediana, lo primero que hay que hacer es ordenar los valores de la variable de forma creciente, y escribir los valores de las frecuencias acumuladas Fi.

Distinguiremos dos casos, datos no agrupados y datos agrupados.

Para datos no agrupados

Se calcula primero el 50% de la población N/2, se lleva ese valor a la columna de frecuencias absolutas acumuladas.

Si el valor no está en la columna de acumuladas, se toma como valor de la mediana el de la variable correspondiente al siguiente.

Si el valor si está en la columna de acumuladas, se toma como mediana la media aritmética del valor de la variable y el siguiente.

Para datos agrupados en intervalos

Se calcula como antes la mitad de la población, y se lleva ese valor a la columna de frecuencias absolutas acumuladas.

Si el valor no está en la columna, se toma como intervalo al que pertenece la Mediana el siguiente al valor de N/2, y después de situarnos en el intervalo por la hipótesis de uniformidad hacemos una proporción entre la amplitud del intervalo, los elementos que tiene y la amplitud que correspondería a la diferencia entre N/2 y la frecuencia acumulada anterior valor que añadiríamos al extremo inferior del intervalo.

Si el valor sí está en la columna de frecuencias acumuladas, se toma como Mediana el extremo superior del intervalo correspondiente.

También se puede hallar gráficamente con el diagrama correspondiente a las frecuencias absolutas acumuladas.

MEDIA GEOMETRICA

Media Geométrica

Es la raíz N-ésima del producto de los valores de la variable elevado cada uno de ellos a su frecuencia absoluta

Tiene el problema de que su cálculo es muy complicado sobre todo si N es grande.

MEDIA ARMONICA

Media Armónica

Es la media de los valores inversos de la variable, o la inversa de la media aritmética.

La media armónica se utiliza cuando la variable se encuentra medida en términos relativos. Por ejemplo la velocidad.

MEDIA CUADRATICA

Media cuadrática

Es la media de los valores de la variable al cuadrado es decir :

MEDIA ARITMETICA SIMPLE

Media aritmética simple

Se suman de todos los valores de la variable ponderados por sus frecuencias absolutas y dividido todo ello por el número total de observaciones


La media aritmética es siempre el centro de gravedad de la distribución y es siempre un valor que entra dentro del campo de variación de la variable.
Si los datos están agrupados en intervalos se toma la marca de clase de cada intervalo para su cálculo.

MEDIA

puede ser:

La media puede ser :

· Aritmética simple o ponderada
· Media Cuadrática
· Media Geométrica Media Armónica

medidas De tendencia no central

cuartiles

Medidas de tendencia central o promedios

1. Media
2. Mediana
3. Moda

algunos significados

- Población son todos y cada uno de los elementos que se quieren analizar. Puede ser finita o infinita( en realidad las poblaciones infinitas no existen, pero cuando se trata de un número grande se trata como si lo fuera).

- Muestra es un subconjunto de la población o parte de la población que se observa.

- Característica de una población es la propiedad que se estudia.

- Variables es cualquier característica cuantitativa ( tome valor numérico) de una población .

En la estadistica hay dos ramas

Estadistica descriptiva:
por medio de la estructura y compocicion analiza una poblacion o muestra




Estadistica Inferecial:
son todos los comportamientos reales que aparecen gracias a los resultados que se tiene de la muetra:

estadistica descriptiva

es la ciencia que por medio de datos matematicos busca encontrarle razon a los fenomenos de calculo.

tipos de datos

DATOS AGRUPADOS: mas de quince datos y se repiten

NO AGRUPADOS: menos de 15 y se repite .

TABLA SIMPLE: menos de 15 y no se repiten .

TIPOS DE DATOS

HAY VARIOS TIPOS DE DATOS ENTRE LOS QUE LES PODRIA MENSIONAR SE ENCUENTRAN LOS DATOS AGRUPADO, NO AGRUPADOS Y TABLAS SIMPLES

Tabla y distribucion de frecuencia

tabla:
son todos los datos que podemos encontran en cualquier tabla.

distribucion de frecuencias:
son datos agrupados y como sabemos que tienen frecuencia sabemos que es una distrbucion de frecuencias en estas distribuciones podemos encontrar las siglas
XI F INT F.